Learning math fundamentals helps build a strong foundation for more... Show more
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Subjects
Triangle Congruence and Similarity Theorems
Triangle Properties and Classification
Linear Equations and Graphs
Geometric Angle Relationships
Trigonometric Functions and Identities
Equation Solving Techniques
Circle Geometry Fundamentals
Division Operations and Methods
Basic Differentiation Rules
Exponent and Logarithm Properties
Show all topics
Human Organ Systems
Reproductive Cell Cycles
Biological Sciences Subdisciplines
Cellular Energy Metabolism
Autotrophic Energy Processes
Inheritance Patterns and Principles
Biomolecular Structure and Organization
Cell Cycle and Division Mechanics
Cellular Organization and Development
Biological Structural Organization
Show all topics
Chemical Sciences and Applications
Atomic Structure and Composition
Molecular Electron Structure Representation
Atomic Electron Behavior
Matter Properties and Water
Mole Concept and Calculations
Gas Laws and Behavior
Periodic Table Organization
Chemical Thermodynamics Fundamentals
Chemical Bond Types and Properties
Show all topics
European Renaissance and Enlightenment
European Cultural Movements 800-1920
American Revolution Era 1763-1797
American Civil War 1861-1865
Global Imperial Systems
Mongol and Chinese Dynasties
U.S. Presidents and World Leaders
Historical Sources and Documentation
World Wars Era and Impact
World Religious Systems
Show all topics
Classic and Contemporary Novels
Literary Character Analysis
Rhetorical Theory and Practice
Classic Literary Narratives
Reading Analysis and Interpretation
Narrative Structure and Techniques
English Language Components
Influential English-Language Authors
Basic Sentence Structure
Narrative Voice and Perspective
Show all topics
132
•
Dec 27, 2025
•
chloe white
@chloewhite_ljzg
Learning math fundamentals helps build a strong foundation for more... Show more

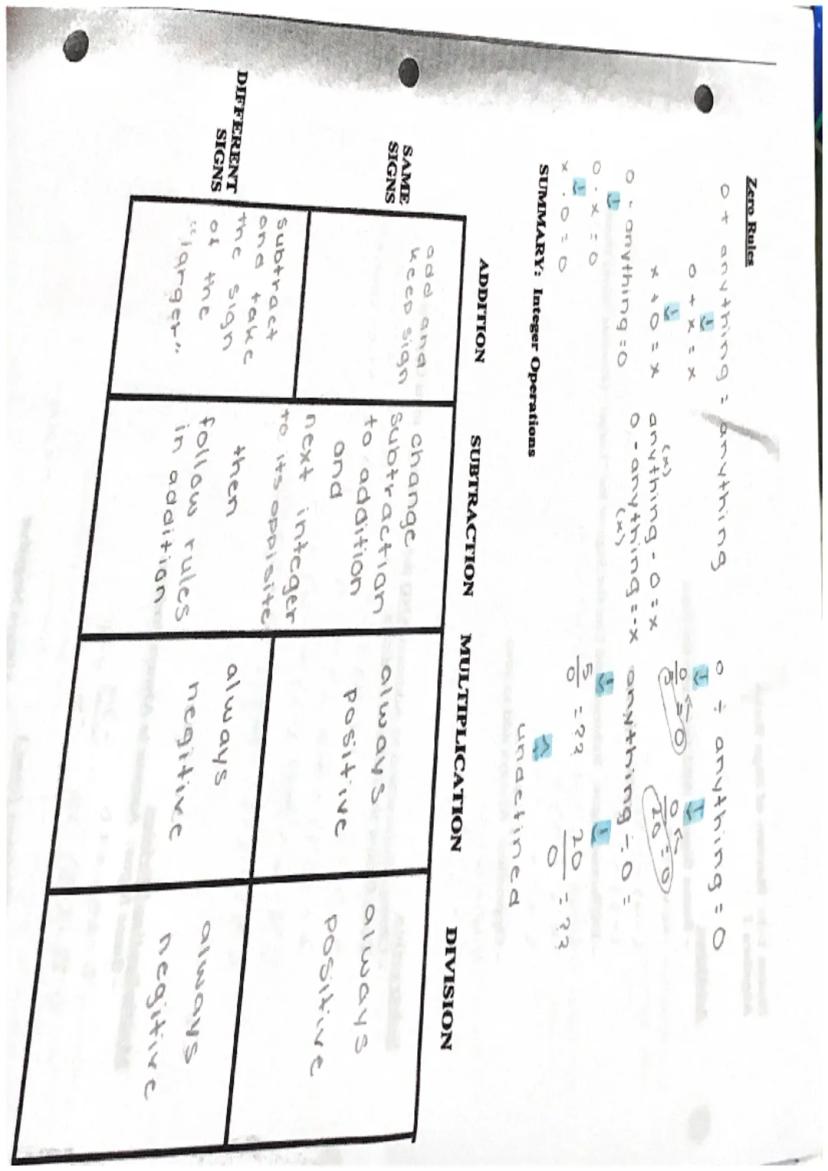








When working with Integer addition and subtraction rules Algebra I, it's essential to master the fundamental sign rules that govern these operations. These rules form the foundation for more complex algebraic concepts.
Addition with integers follows specific patterns based on signs. When adding numbers with the same sign, you simply add the absolute values and keep the common sign. For example, adding two positive numbers like 4 + 3 = 7 works just like regular addition. Similarly, when adding two negative numbers such as (-4) + (-3), you add the absolute values (4 + 3 = 7) and keep the negative sign, giving you -7.
Definition: Absolute value is the positive distance a number is from zero on the number line, regardless of whether the number is positive or negative.
When adding numbers with different signs, subtract the smaller absolute value from the larger absolute value and use the sign of the number with the larger absolute value. For instance, when adding (-4) + 3, the absolute values are 4 and 3. Since 4 is larger and the original number was negative, the result is -1.
For subtraction, the key is to transform it into addition by changing the subtraction sign to addition and taking the opposite of the second number. For example, 4 - 9 becomes 4 + (-9) = -5. This transformation allows you to apply the addition rules you've already learned.

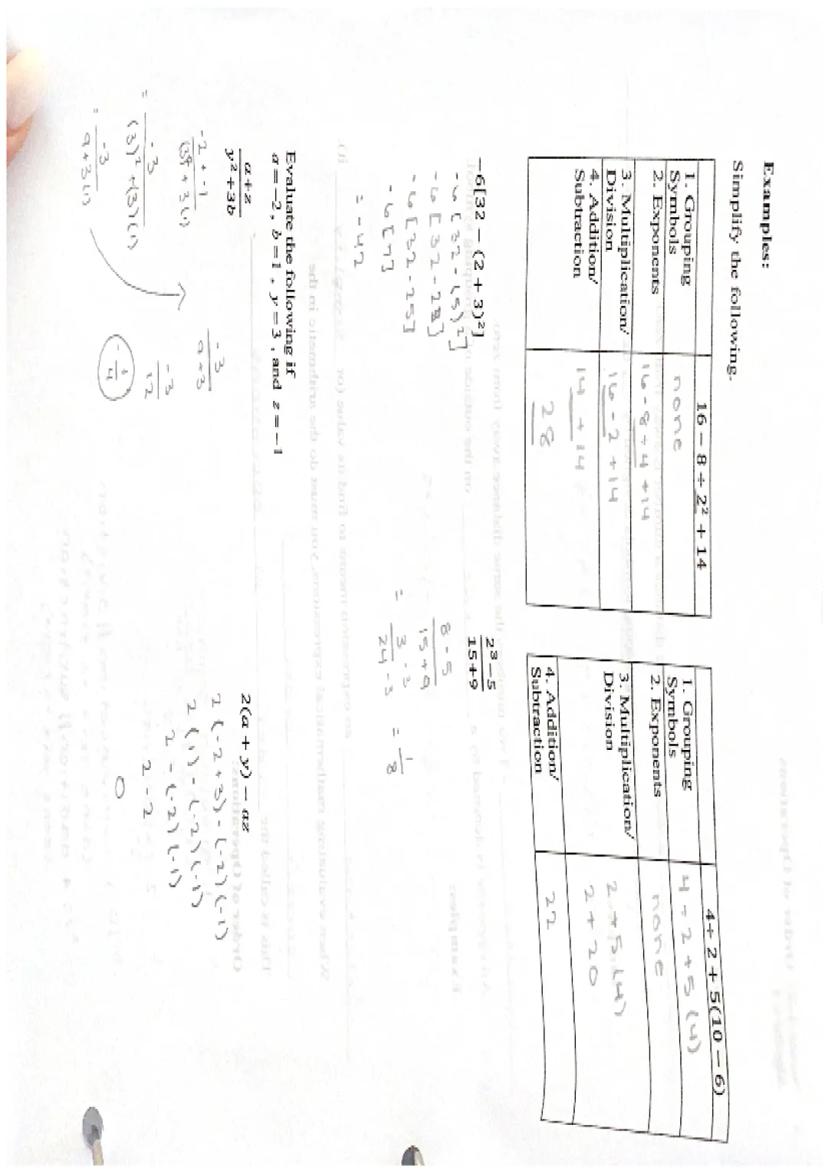
Understanding order of operations in Algebra I is crucial for correctly evaluating mathematical expressions. The sequence of operations must be followed precisely to arrive at the correct answer.
Vocabulary: PEMDAS is the standard order of operations used in algebra.
The order begins with grouping symbols (parentheses, brackets, and braces), followed by exponents. After handling these, multiplication and division are performed from left to right, followed by addition and subtraction, also from left to right. This systematic approach ensures consistency in mathematical calculations.
When evaluating expressions with variables, substitute the given values for variables first, then follow the order of operations. For example, if evaluating 2 - az where a = 2, x = 3, and z = -1, first substitute the values, then solve step by step following PEMDAS.

Converting fractions, decimals, and percents in algebra requires understanding the relationship between these different numerical representations. This knowledge is fundamental for solving complex algebraic problems.
Example: To convert a fraction to a decimal, divide the numerator by the denominator. For instance, 3/4 = 0.75
When working with mixed numbers in algebraic expressions, it's important to convert them to improper fractions before performing operations. This ensures accurate calculations and helps avoid common mistakes in algebraic manipulations.
Understanding equivalent forms of numbers allows for strategic problem-solving in algebra. Sometimes, converting between fractions, decimals, and percents can simplify calculations or make patterns more apparent.

The principles of integer operations extend beyond basic calculations into more complex algebraic concepts. Understanding these fundamentals is crucial for success in higher-level mathematics.
Highlight: When multiplying or dividing integers, remember: same signs yield a positive result, different signs yield a negative result.
These rules apply consistently across all algebraic operations, including work with polynomials and rational expressions. For example, when multiplying binomials with negative terms, these same sign rules help determine the signs of each term in the product.
The practical applications of integer operations appear in many real-world scenarios, from calculating temperature changes to managing financial transactions. Understanding these concepts helps students develop strong problem-solving skills applicable to both academic and real-world situations.

Converting fractions, decimals, and percents in algebra is a fundamental skill that builds the foundation for more advanced mathematical concepts. Let's break down these essential conversions and explore square roots in detail.
Definition: A conversion in mathematics means changing the form of a number while maintaining its value. For example, 0.5 is equal to 1/2 and 50% - these are different representations of the same quantity.
When converting decimals to percents, move the decimal point two places to the right and add the percent symbol. For instance, 0.34 becomes 34%, and 0.70 becomes 70%. This process works because percent literally means "per hundred," so we're expressing the decimal as parts per hundred.
Converting decimals to fractions requires careful attention to place value. Write the decimal as a fraction over the appropriate power of ten based on decimal places, then simplify. For example, 0.36 becomes 36/100, which simplifies to 9/25. This works because decimal places represent divisions by powers of ten.
Example: To convert 0.125 to a fraction:

Understanding square roots is crucial in Understanding order of operations in Algebra I. A square root is the inverse operation of squaring a number, represented by the radical symbol (√).
Vocabulary: A perfect square is a number that has an integer square root. For example, 16 is a perfect square because √16 = 4.
Perfect squares form a pattern: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100. Recognizing these numbers helps in simplifying square roots. When working with non-perfect squares, we can approximate their values by identifying the perfect squares on either side.
The principal square root is always positive, even though numbers can have both positive and negative square roots. For example, while both 4 and -4 square to give 16, we consider √16 = 4 as the principal square root.
Highlight: When approximating square roots, look for the perfect squares on either side of the number and estimate between them. For example, √50 lies between √49 (=7) and √64 (=8).

A systematic approach to comparing and ordering numbers is essential in Integer addition and subtraction rules Algebra I. This process involves converting numbers to a common format for accurate comparison.
When comparing different types of numbers (decimals, fractions, and integers), convert them to the same format first. Typically, converting to decimals makes comparison easier, but sometimes using fractions is more appropriate, especially with repeating decimals.
Definition: Rational numbers are numbers that can be expressed as a ratio of two integers. This includes all integers, fractions, and terminating or repeating decimals.
To order numbers from least to greatest:
Example: Ordering -2, 1.5, -√4, 3/2:

Understanding how different number representations interact is crucial for success in algebra. This knowledge forms the foundation for solving complex equations and word problems.
When working with mixed operations involving fractions, decimals, and percents, convert all numbers to the same format before proceeding. This ensures accurate calculations and helps avoid common errors in mathematical operations.
Highlight: Always verify your conversions by cross-checking. For example, if you convert 3/4 to 0.75 to 75%, all three forms should be equivalent.
The ability to move fluently between different number representations is particularly valuable in real-world applications, such as financial calculations, scientific measurements, and statistical analysis. This skill becomes increasingly important in higher-level mathematics and practical applications.
Example: In financial calculations, you might need to:

Estimation is a fundamental mathematical skill that helps students solve problems quickly by using approximate values instead of exact calculations. When working with Understanding order of operations in Algebra I, estimation becomes an essential tool for checking whether answers are reasonable.
The process of estimation follows three key steps: First, carefully read and understand the problem. Second, round the numbers to make calculations more manageable. Third, use mental math to solve the problem with the rounded numbers. This systematic approach helps students develop number sense and mathematical intuition.
Definition: Estimation is the process of finding an approximate value that's close enough to the exact answer for a specific purpose.
Let's examine how estimation works in real-world scenarios. Consider a problem involving ticket sales at a state final game. If 6,556 total tickets were sold and 1,247 went to the opposing team's fans, we can estimate the home team's fans by rounding to the nearest thousand. 6,556 rounds to 7,000, and 1,247 rounds to 1,000. The estimated difference of 6,000 tickets represents the home team's fans.
Example: When estimating 361 × 32:

When dealing with more complex calculations involving Integer addition and subtraction rules Algebra I, estimation becomes particularly valuable. For instance, when working with multiple numbers in addition problems, rounding to the nearest hundred can simplify calculations while maintaining reasonable accuracy.
Highlight: When estimating with decimals and fractions, round to the nearest whole number first, then apply the necessary operations.
Students should understand that estimation serves multiple purposes in algebra. It helps verify calculator results, provides quick approximations for real-world problems, and develops mental math skills. When Converting fractions, decimals, and percents in algebra, estimation can help students quickly check if their conversions make sense.
The level of precision needed in estimation depends on the context. In some cases, rounding to the nearest thousand is sufficient, while other situations might require rounding to the nearest hundred or ten. The key is understanding the problem's requirements and choosing an appropriate level of estimation.
Vocabulary: Mental Math - The process of performing calculations in your head without using paper, calculator, or other tools.
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
You can download the app in the Google Play Store and in the Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
chloe white
@chloewhite_ljzg
Learning math fundamentals helps build a strong foundation for more advanced concepts.
Integer addition and subtraction rules Algebra Iform the basis for working with positive and negative numbers. When adding integers with the same sign, add the absolute values... Show more

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
When working with Integer addition and subtraction rules Algebra I, it's essential to master the fundamental sign rules that govern these operations. These rules form the foundation for more complex algebraic concepts.
Addition with integers follows specific patterns based on signs. When adding numbers with the same sign, you simply add the absolute values and keep the common sign. For example, adding two positive numbers like 4 + 3 = 7 works just like regular addition. Similarly, when adding two negative numbers such as (-4) + (-3), you add the absolute values (4 + 3 = 7) and keep the negative sign, giving you -7.
Definition: Absolute value is the positive distance a number is from zero on the number line, regardless of whether the number is positive or negative.
When adding numbers with different signs, subtract the smaller absolute value from the larger absolute value and use the sign of the number with the larger absolute value. For instance, when adding (-4) + 3, the absolute values are 4 and 3. Since 4 is larger and the original number was negative, the result is -1.
For subtraction, the key is to transform it into addition by changing the subtraction sign to addition and taking the opposite of the second number. For example, 4 - 9 becomes 4 + (-9) = -5. This transformation allows you to apply the addition rules you've already learned.

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Understanding order of operations in Algebra I is crucial for correctly evaluating mathematical expressions. The sequence of operations must be followed precisely to arrive at the correct answer.
Vocabulary: PEMDAS is the standard order of operations used in algebra.
The order begins with grouping symbols (parentheses, brackets, and braces), followed by exponents. After handling these, multiplication and division are performed from left to right, followed by addition and subtraction, also from left to right. This systematic approach ensures consistency in mathematical calculations.
When evaluating expressions with variables, substitute the given values for variables first, then follow the order of operations. For example, if evaluating 2 - az where a = 2, x = 3, and z = -1, first substitute the values, then solve step by step following PEMDAS.

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Converting fractions, decimals, and percents in algebra requires understanding the relationship between these different numerical representations. This knowledge is fundamental for solving complex algebraic problems.
Example: To convert a fraction to a decimal, divide the numerator by the denominator. For instance, 3/4 = 0.75
When working with mixed numbers in algebraic expressions, it's important to convert them to improper fractions before performing operations. This ensures accurate calculations and helps avoid common mistakes in algebraic manipulations.
Understanding equivalent forms of numbers allows for strategic problem-solving in algebra. Sometimes, converting between fractions, decimals, and percents can simplify calculations or make patterns more apparent.

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
The principles of integer operations extend beyond basic calculations into more complex algebraic concepts. Understanding these fundamentals is crucial for success in higher-level mathematics.
Highlight: When multiplying or dividing integers, remember: same signs yield a positive result, different signs yield a negative result.
These rules apply consistently across all algebraic operations, including work with polynomials and rational expressions. For example, when multiplying binomials with negative terms, these same sign rules help determine the signs of each term in the product.
The practical applications of integer operations appear in many real-world scenarios, from calculating temperature changes to managing financial transactions. Understanding these concepts helps students develop strong problem-solving skills applicable to both academic and real-world situations.

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Converting fractions, decimals, and percents in algebra is a fundamental skill that builds the foundation for more advanced mathematical concepts. Let's break down these essential conversions and explore square roots in detail.
Definition: A conversion in mathematics means changing the form of a number while maintaining its value. For example, 0.5 is equal to 1/2 and 50% - these are different representations of the same quantity.
When converting decimals to percents, move the decimal point two places to the right and add the percent symbol. For instance, 0.34 becomes 34%, and 0.70 becomes 70%. This process works because percent literally means "per hundred," so we're expressing the decimal as parts per hundred.
Converting decimals to fractions requires careful attention to place value. Write the decimal as a fraction over the appropriate power of ten based on decimal places, then simplify. For example, 0.36 becomes 36/100, which simplifies to 9/25. This works because decimal places represent divisions by powers of ten.
Example: To convert 0.125 to a fraction:

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Understanding square roots is crucial in Understanding order of operations in Algebra I. A square root is the inverse operation of squaring a number, represented by the radical symbol (√).
Vocabulary: A perfect square is a number that has an integer square root. For example, 16 is a perfect square because √16 = 4.
Perfect squares form a pattern: 1, 4, 9, 16, 25, 36, 49, 64, 81, 100. Recognizing these numbers helps in simplifying square roots. When working with non-perfect squares, we can approximate their values by identifying the perfect squares on either side.
The principal square root is always positive, even though numbers can have both positive and negative square roots. For example, while both 4 and -4 square to give 16, we consider √16 = 4 as the principal square root.
Highlight: When approximating square roots, look for the perfect squares on either side of the number and estimate between them. For example, √50 lies between √49 (=7) and √64 (=8).

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
A systematic approach to comparing and ordering numbers is essential in Integer addition and subtraction rules Algebra I. This process involves converting numbers to a common format for accurate comparison.
When comparing different types of numbers (decimals, fractions, and integers), convert them to the same format first. Typically, converting to decimals makes comparison easier, but sometimes using fractions is more appropriate, especially with repeating decimals.
Definition: Rational numbers are numbers that can be expressed as a ratio of two integers. This includes all integers, fractions, and terminating or repeating decimals.
To order numbers from least to greatest:
Example: Ordering -2, 1.5, -√4, 3/2:

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Understanding how different number representations interact is crucial for success in algebra. This knowledge forms the foundation for solving complex equations and word problems.
When working with mixed operations involving fractions, decimals, and percents, convert all numbers to the same format before proceeding. This ensures accurate calculations and helps avoid common errors in mathematical operations.
Highlight: Always verify your conversions by cross-checking. For example, if you convert 3/4 to 0.75 to 75%, all three forms should be equivalent.
The ability to move fluently between different number representations is particularly valuable in real-world applications, such as financial calculations, scientific measurements, and statistical analysis. This skill becomes increasingly important in higher-level mathematics and practical applications.
Example: In financial calculations, you might need to:

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Estimation is a fundamental mathematical skill that helps students solve problems quickly by using approximate values instead of exact calculations. When working with Understanding order of operations in Algebra I, estimation becomes an essential tool for checking whether answers are reasonable.
The process of estimation follows three key steps: First, carefully read and understand the problem. Second, round the numbers to make calculations more manageable. Third, use mental math to solve the problem with the rounded numbers. This systematic approach helps students develop number sense and mathematical intuition.
Definition: Estimation is the process of finding an approximate value that's close enough to the exact answer for a specific purpose.
Let's examine how estimation works in real-world scenarios. Consider a problem involving ticket sales at a state final game. If 6,556 total tickets were sold and 1,247 went to the opposing team's fans, we can estimate the home team's fans by rounding to the nearest thousand. 6,556 rounds to 7,000, and 1,247 rounds to 1,000. The estimated difference of 6,000 tickets represents the home team's fans.
Example: When estimating 361 × 32:

Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
When dealing with more complex calculations involving Integer addition and subtraction rules Algebra I, estimation becomes particularly valuable. For instance, when working with multiple numbers in addition problems, rounding to the nearest hundred can simplify calculations while maintaining reasonable accuracy.
Highlight: When estimating with decimals and fractions, round to the nearest whole number first, then apply the necessary operations.
Students should understand that estimation serves multiple purposes in algebra. It helps verify calculator results, provides quick approximations for real-world problems, and develops mental math skills. When Converting fractions, decimals, and percents in algebra, estimation can help students quickly check if their conversions make sense.
The level of precision needed in estimation depends on the context. In some cases, rounding to the nearest thousand is sufficient, while other situations might require rounding to the nearest hundred or ten. The key is understanding the problem's requirements and choosing an appropriate level of estimation.
Vocabulary: Mental Math - The process of performing calculations in your head without using paper, calculator, or other tools.
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
You can download the app in the Google Play Store and in the Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
6
Smart Tools NEW
Transform this note into: ✓ 50+ Practice Questions ✓ Interactive Flashcards ✓ Full Mock Exam ✓ Essay Outlines
Learn how to do ratios
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user