Biology
Chemistry
AP Chemistry
English
AP English Literature
39
•
Dec 7, 2025
•
Navigating through Pre-Calculus trigonometry might seem challenging at first, but... Show more
Ever wondered how mathematicians describe angles in different ways? Angles can be located in different quadrants of the coordinate plane, with each location affecting trigonometric values.
When working with angles, knowing the reference angle helps simplify calculations. The reference angle is always the positive acute angle formed between the terminal side and the x-axis. For example, a 220° angle falls in the third quadrant, and its reference angle would be 40°.
Finding coterminal angles is another important skill—these are angles that share the same terminal side. To find coterminal angles, simply add or subtract 360° (or 2π radians) as needed.
💡 Quick Tip: When a point (x,y) is on the terminal side of an angle in standard position, you can find all six trig functions using these relationships: sin θ = y/r, cos θ = x/r, and tan θ = y/x, where r = √.
If you know one trigonometric value and the quadrant, you can determine all other values. For instance, if tan θ = -24/7 and cos θ < 0, you know the angle is in the second quadrant, which gives you the information needed to find sin θ, csc θ, sec θ, and cot θ.
Ready to apply what you've learned? Evaluating trigonometric functions for special angles becomes easier when you understand how reference angles work. For angles like -60°, 4π/3, or 810°, first find the reference angle and quadrant, then determine the sign.
Trigonometry isn't just abstract math—it solves real problems! When calculating the arc length of a circle, use the formula s = rθ where r is the radius and θ is the central angle in radians. For a clock with a 16-inch radius and a 145° rotation, you'd convert the angle to radians first.
Angle of elevation problems help you find heights using trigonometry. If you're 3 meters from a tree looking up at an angle of 38.9°, you can use tan(38.9°) = height/3 to find the tree's height.
🔍 Real-world connection: Surveyors, engineers, and architects use these exact same trigonometric principles to measure heights of buildings, distances across rivers, and angles for construction projects!
Converting between degrees and radians is essential in trigonometry. Remember that 180° = π radians, so to convert from radians to degrees, multiply by 180°/π, and to convert from degrees to radians, multiply by π/180°.
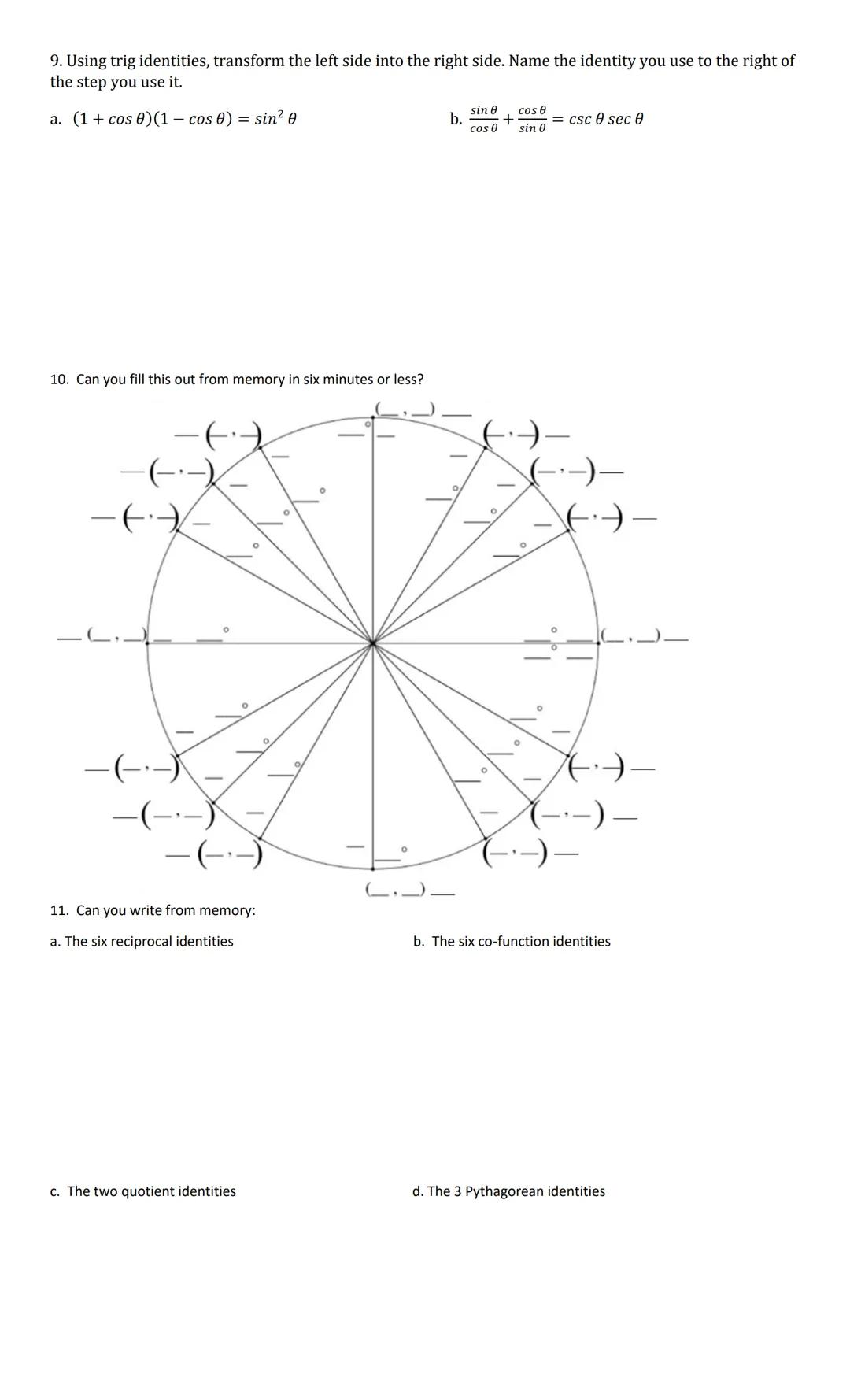
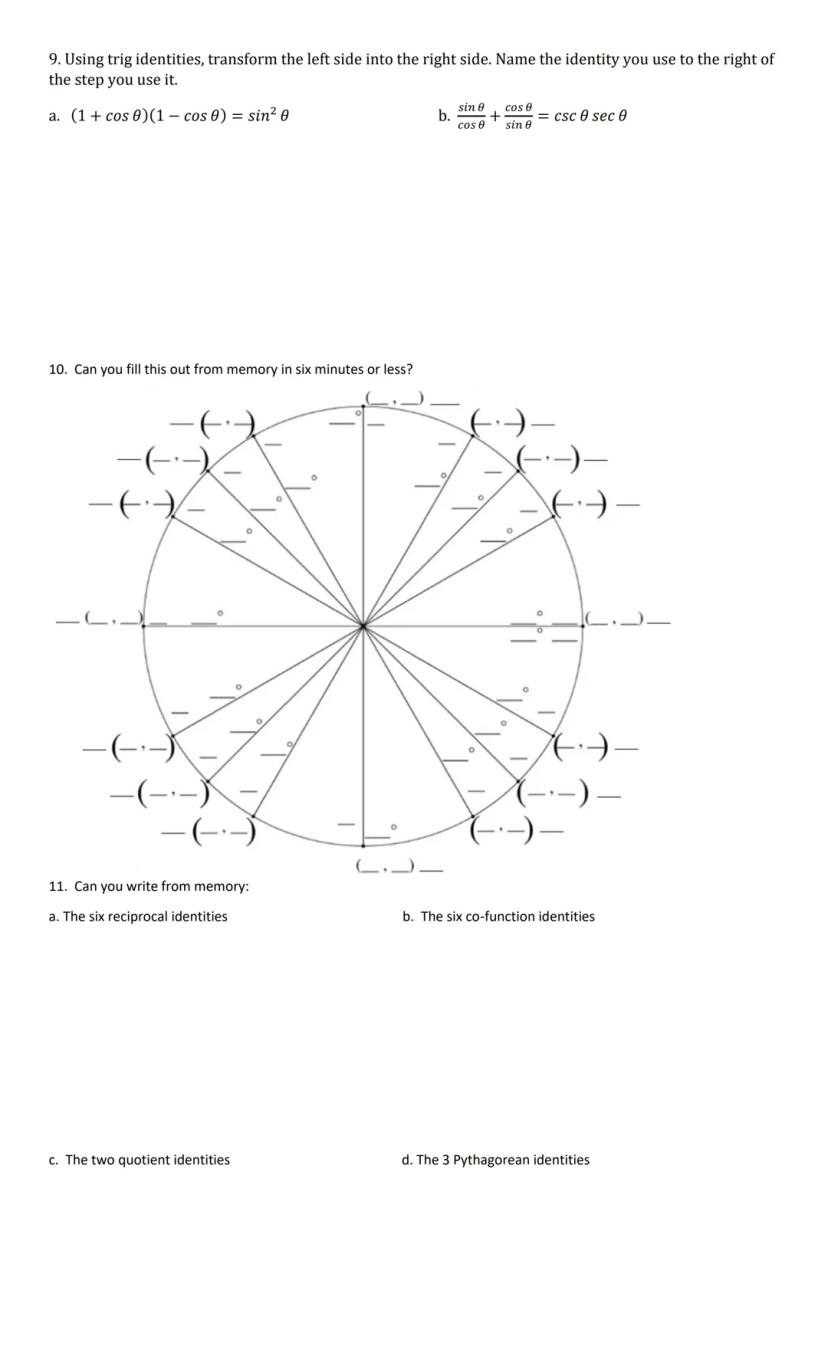
Trigonometric identities are powerful formulas that help simplify complex expressions. When transforming expressions like into sin² θ, you'll need to apply identities systematically to reach your goal.
The most fundamental identities you should memorize fall into four categories:
💪 Challenge yourself: Spend six minutes each day trying to write all the identities from memory. This practice will make solving complex trig problems much faster on tests!
Understanding these identities isn't about memorization alone—it's about seeing how all trigonometric functions relate to each other. Once you grasp these connections, you'll be able to tackle even the most complicated trigonometry problems with confidence.
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
You can download the app in the Google Play Store and in the Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
App Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
Navigating through Pre-Calculus trigonometry might seem challenging at first, but it's all about understanding patterns and relationships between angles and functions. This review covers key concepts including angle measurements, trigonometric functions, and practical applications that you'll need to master for... Show more
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Ever wondered how mathematicians describe angles in different ways? Angles can be located in different quadrants of the coordinate plane, with each location affecting trigonometric values.
When working with angles, knowing the reference angle helps simplify calculations. The reference angle is always the positive acute angle formed between the terminal side and the x-axis. For example, a 220° angle falls in the third quadrant, and its reference angle would be 40°.
Finding coterminal angles is another important skill—these are angles that share the same terminal side. To find coterminal angles, simply add or subtract 360° (or 2π radians) as needed.
💡 Quick Tip: When a point (x,y) is on the terminal side of an angle in standard position, you can find all six trig functions using these relationships: sin θ = y/r, cos θ = x/r, and tan θ = y/x, where r = √.
If you know one trigonometric value and the quadrant, you can determine all other values. For instance, if tan θ = -24/7 and cos θ < 0, you know the angle is in the second quadrant, which gives you the information needed to find sin θ, csc θ, sec θ, and cot θ.
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Ready to apply what you've learned? Evaluating trigonometric functions for special angles becomes easier when you understand how reference angles work. For angles like -60°, 4π/3, or 810°, first find the reference angle and quadrant, then determine the sign.
Trigonometry isn't just abstract math—it solves real problems! When calculating the arc length of a circle, use the formula s = rθ where r is the radius and θ is the central angle in radians. For a clock with a 16-inch radius and a 145° rotation, you'd convert the angle to radians first.
Angle of elevation problems help you find heights using trigonometry. If you're 3 meters from a tree looking up at an angle of 38.9°, you can use tan(38.9°) = height/3 to find the tree's height.
🔍 Real-world connection: Surveyors, engineers, and architects use these exact same trigonometric principles to measure heights of buildings, distances across rivers, and angles for construction projects!
Converting between degrees and radians is essential in trigonometry. Remember that 180° = π radians, so to convert from radians to degrees, multiply by 180°/π, and to convert from degrees to radians, multiply by π/180°.
Access to all documents
Improve your grades
Join milions of students
By signing up you accept Terms of Service and Privacy Policy
Trigonometric identities are powerful formulas that help simplify complex expressions. When transforming expressions like into sin² θ, you'll need to apply identities systematically to reach your goal.
The most fundamental identities you should memorize fall into four categories:
💪 Challenge yourself: Spend six minutes each day trying to write all the identities from memory. This practice will make solving complex trig problems much faster on tests!
Understanding these identities isn't about memorization alone—it's about seeing how all trigonometric functions relate to each other. Once you grasp these connections, you'll be able to tackle even the most complicated trigonometry problems with confidence.
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
You can download the app in the Google Play Store and in the Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
2
Smart Tools NEW
Transform this note into: ✓ 50+ Practice Questions ✓ Interactive Flashcards ✓ Full Mock Exam ✓ Essay Outlines
This is an assignment about Pre-Calculus.
Pre-CalculusThis is an assignment about reviewing precal
Pre-CalculusThis is about proving of trigonometric identities and solutions of right triangles' problems.
Pre-CalculusApp Store
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE THE SCHOOLGPT. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
Algebra 2
Trigonometry
Calculus 1
Algebra 1
Overige