Ready to conquer polynomial functions? This chapter dives into quadratic... Show more
Algebra 1
AlgebraSign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
224
•
Feb 6, 2026
•
Understanding Polynomial and Rational Functions
sumehra
@sumehra
1 / 6
Quadratic Functions Basics
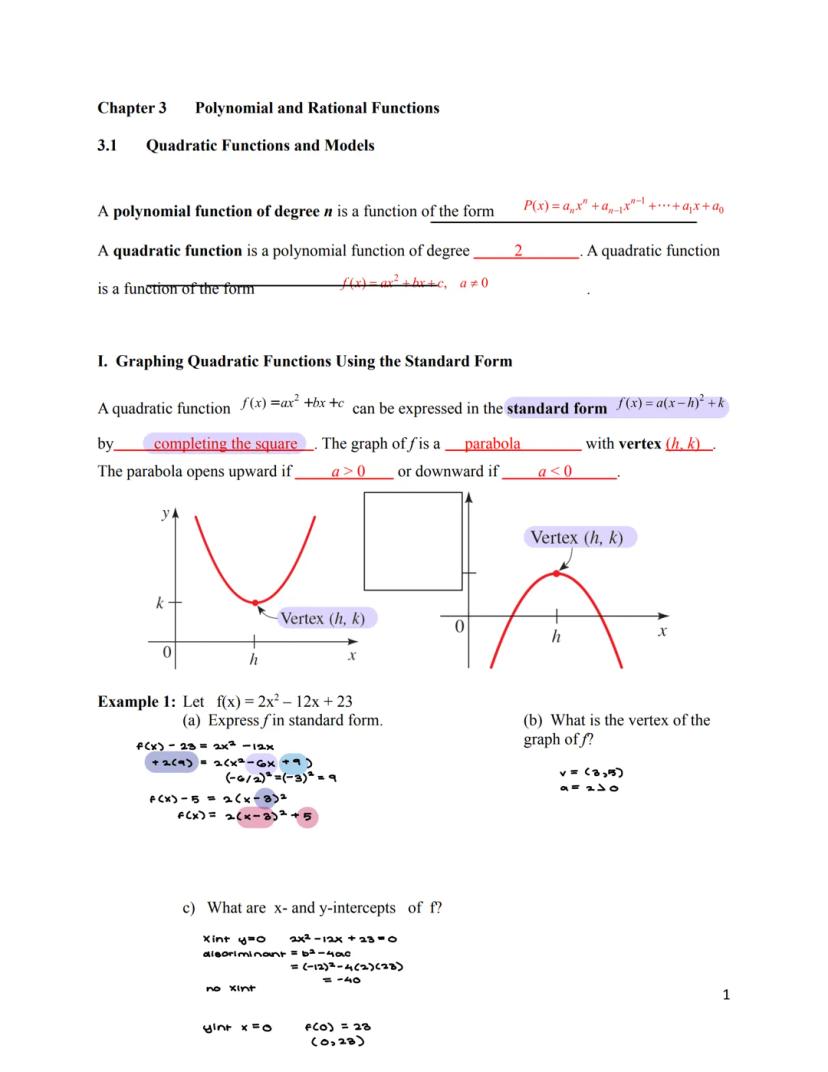
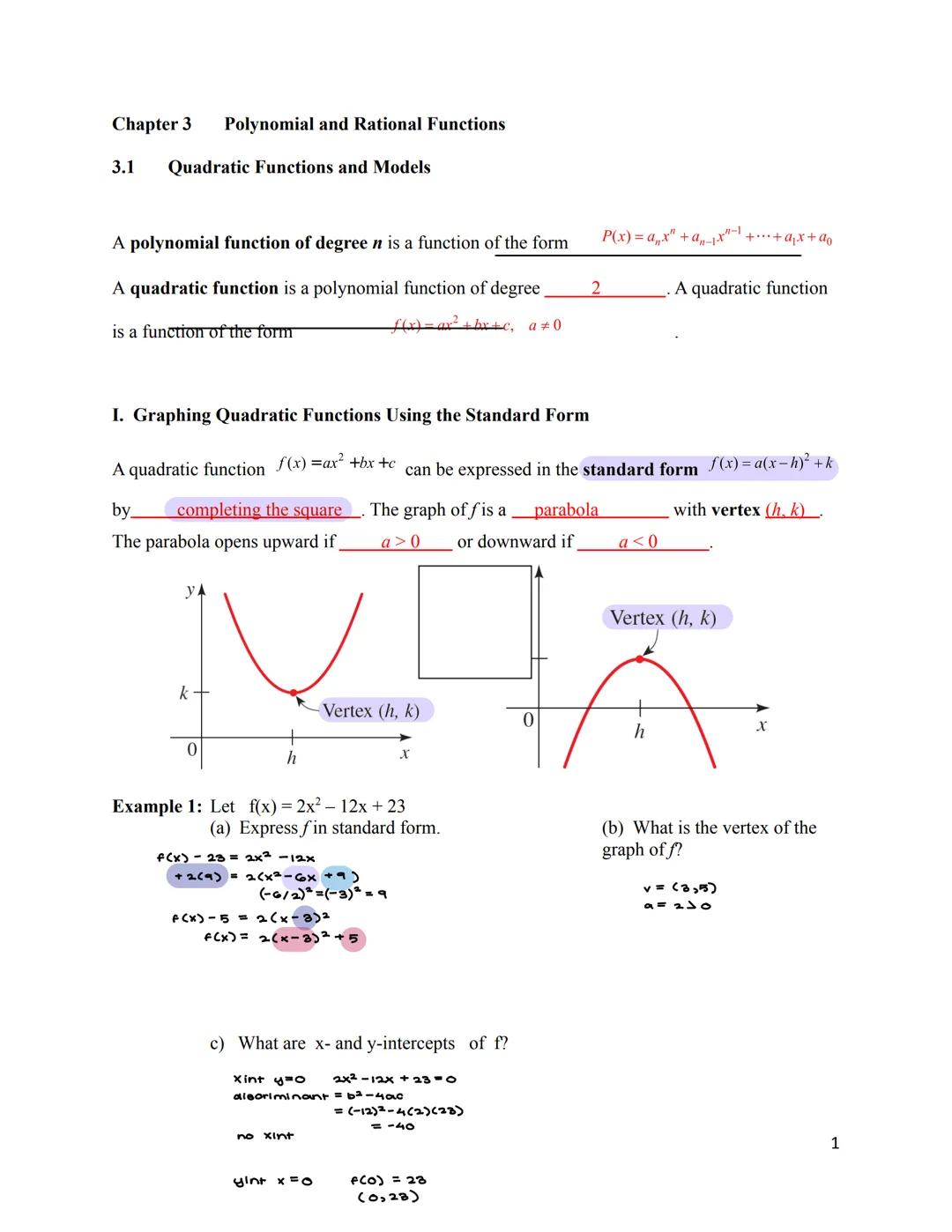
A quadratic function has the form f(x) = ax² + bx + c where a ≠ 0. Every quadratic function creates a U-shaped curve called a parabola when graphed. The standard form f(x) = a² + k tells you exactly where the parabola's lowest (or highest) point is.
The point (h, k) is called the vertex of the parabola. When a > 0, the parabola opens upward like a cup. When a < 0, it opens downward like an upside-down cup. Finding the vertex is crucial because it represents either the minimum or maximum value of the function.
To convert from general form to standard form, you need to "complete the square." This involves rearranging terms and adding/subtracting values to create a perfect square trinomial.
💡 Think of the standard form as giving you GPS coordinates for the vertex. The h tells you to go left/right, and the k tells you how high/low the vertex sits!
Graphing Quadratic Functions
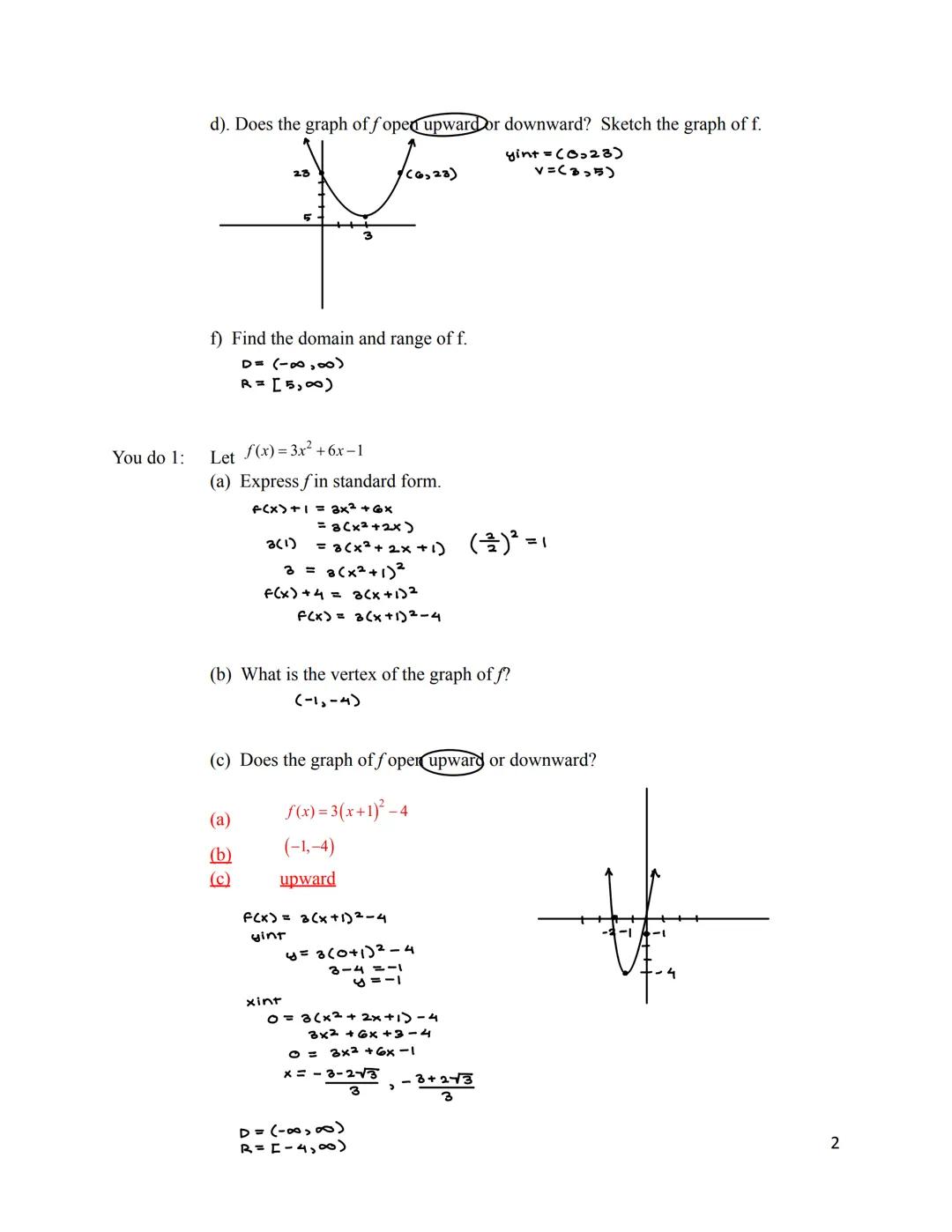
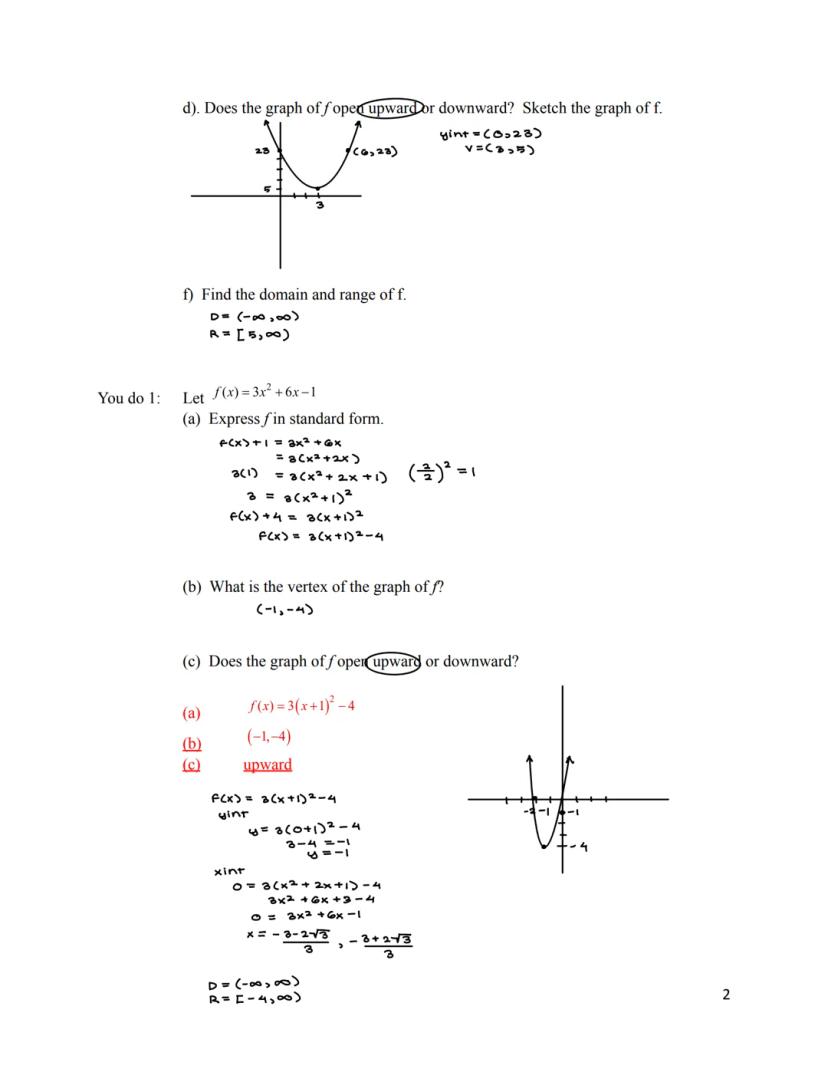
When graphing a quadratic function, finding key points makes the process much easier. Start with the vertex - it's the turning point of your parabola. Then find the y-intercept by plugging in x = 0, which tells you where the parabola crosses the y-axis.
The x-intercepts can be found by setting f(x) = 0 and solving the equation. Not all quadratic functions have x-intercepts - it depends on whether the discriminant is positive, zero, or negative.
The domain of a quadratic function is always all real numbers (-∞, ∞), meaning you can input any value for x. The range depends on whether the parabola opens up or down. If it opens up, the range is .
🔍 Missing x-intercepts? Check the discriminant! If b² - 4ac < 0, your parabola never crosses the x-axis.
Maximum and Minimum Values
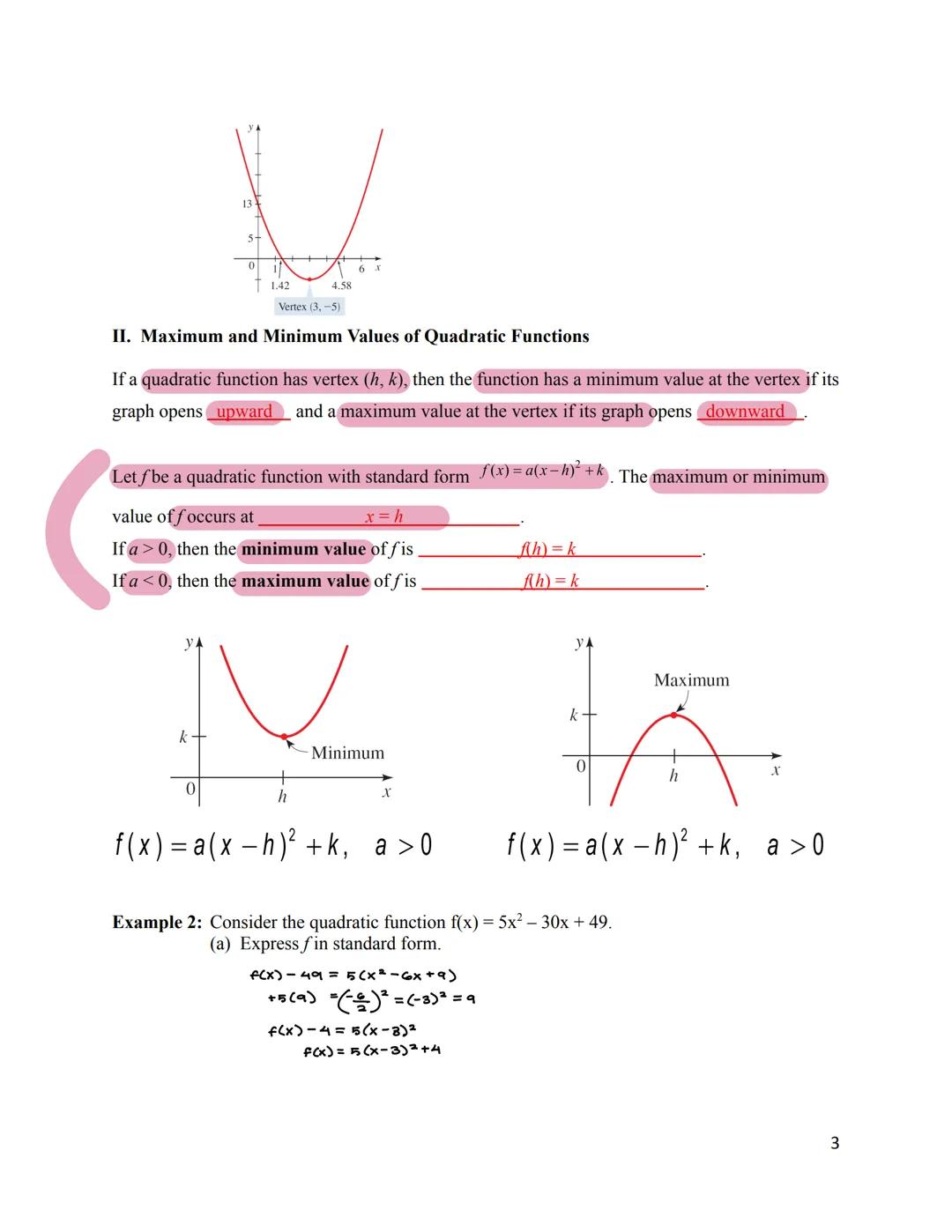
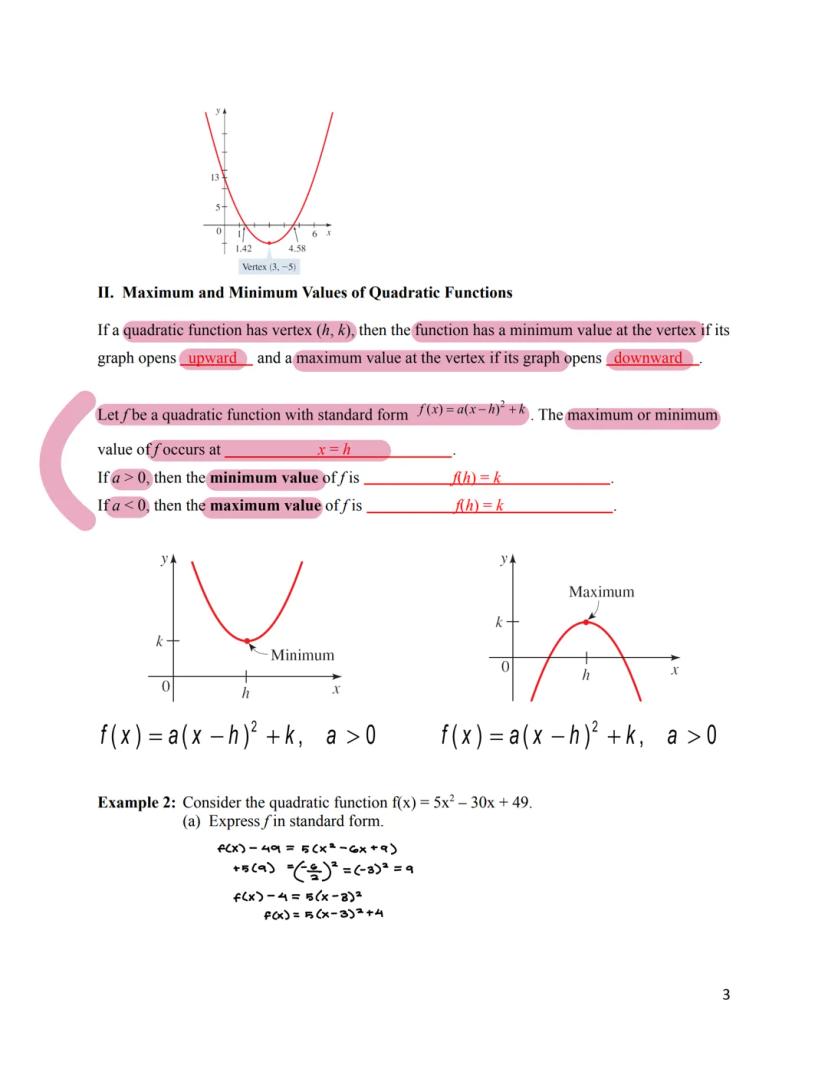
One of the most useful features of quadratic functions is their ability to model maximum or minimum values. The vertex (h, k) is where these extreme values occur. This is incredibly helpful for optimization problems!
If a > 0 (parabola opens upward), the function has a minimum value of k at x = h. This means the output value can never go below k. If a < 0 (parabola opens downward), the function has a maximum value of k at x = h, meaning the output can never exceed k.
For a quadratic function in standard form f(x) = a² + k, you can immediately identify whether it has a maximum or minimum and what that value is. This is why converting to standard form is so important in applications.
⭐ Remember: In any optimization problem involving a quadratic function, the vertex gives you the answer! It's either the maximum or minimum value you're looking for.
Finding Maximum and Minimum Values
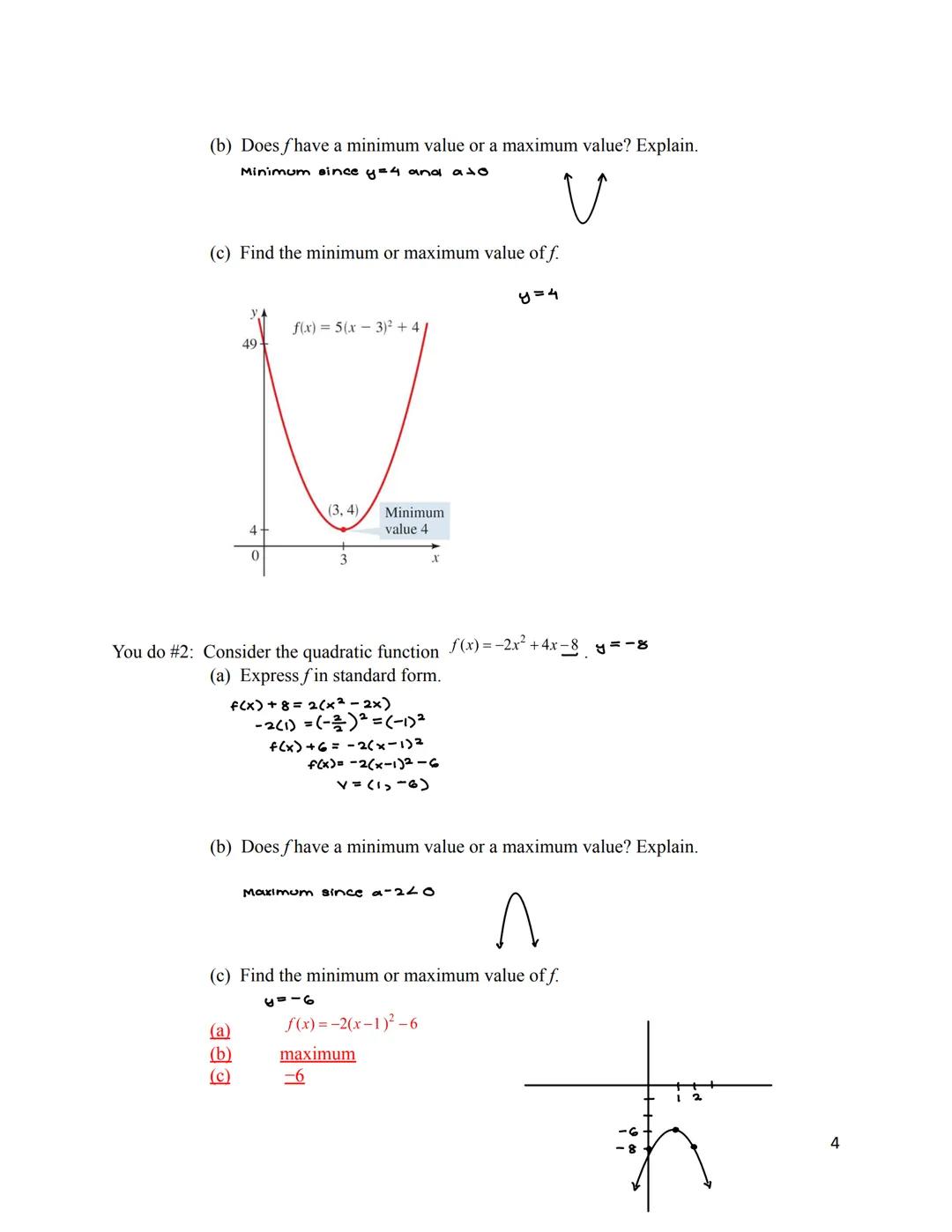
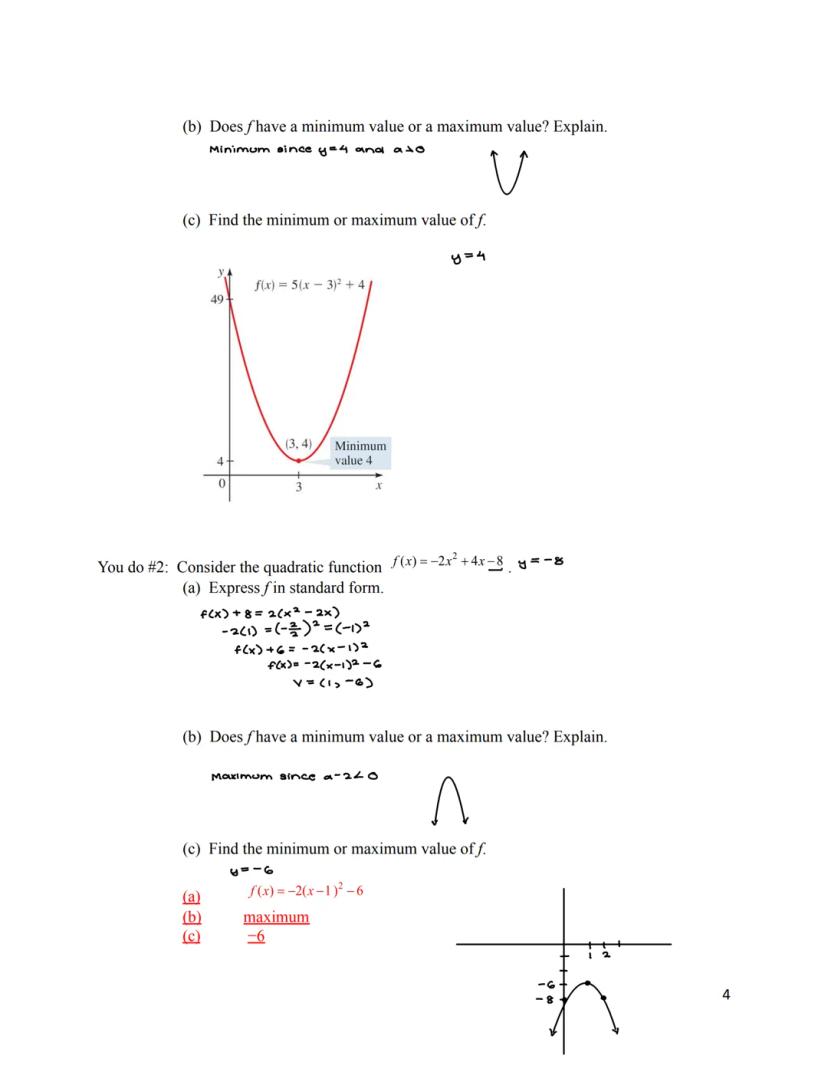
When given a quadratic function in general form f(x) = ax² + bx + c, you can find the maximum or minimum without converting to standard form. The x-value where this occurs is always at x = -b/(2a).
To find the actual maximum or minimum value, simply evaluate the function at this x-value. If a > 0, you've found the minimum value. If a < 0, you've found the maximum value.
This shortcut is incredibly useful for test questions and real-world problems. Instead of going through the entire process of converting to standard form, you can quickly identify where the extreme value occurs and what that value is.
🚀 Quick tip: The formula x = -b/(2a) is a time-saver on tests! Memorize it to find the vertex x-coordinate without completing the square.
Application and Modeling
Quadratic functions appear everywhere in the real world! From the path of a thrown ball to profit models, these functions help us analyze situations where values increase and then decrease (or vice versa).
When working with application problems, identify the quantities being related and set up a quadratic function. Then find the maximum or minimum using the techniques we've learned. The vertex will often represent the optimal solution - like the maximum height of a projectile or the minimum cost of production.
For optimization problems, remember to check if any constraints exist. Sometimes the mathematical maximum or minimum might fall outside the practical range of values for the situation.
🌟 Real-life connection: Gas mileage often follows a quadratic pattern - too slow or too fast both waste fuel, while a medium speed maximizes efficiency!
Real-World Applications
Quadratic functions are perfect for modeling situations with a clear maximum or minimum. For example, the gas mileage problem shows how efficiency first increases with speed, reaches an optimal point, then decreases at higher speeds.
In the car example, the gas mileage function M(s) = -1/28s² + 3s - 31 models the relationship between speed (s) and miles per gallon (M). By finding the vertex, we can determine the optimal speed for maximum efficiency.
To solve such problems, identify the coefficient values (a, b, c) and use the formula x = -b/(2a) to find where the maximum or minimum occurs. Then substitute this value back into the original function to find the optimal result.
🚗 Next time you're driving, remember that your car's optimal fuel efficiency isn't at the lowest or highest speed, but somewhere in the middle - just like a quadratic function predicts!
We thought you’d never ask...
What is the Knowunity AI companion?
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
Where can I download the Knowunity app?
You can download the app in the Google Play Store and in the Apple App Store.
Is Knowunity really free of charge?
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
Most popular content: Standard Form of a Parabola
Most popular content in Algebra 1
Most popular content
Can't find what you're looking for? Explore other subjects.
Students love us — and so will you.
4.6/5
App Store
4.7/5
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
Understanding Polynomial and Rational Functions
sumehra
@sumehra
Ready to conquer polynomial functions? This chapter dives into quadratic functions - those x² expressions that create parabolas on graphs. Understanding these functions helps you analyze real-world situations like maximum heights, minimum costs, and optimal speeds.
Quadratic Functions Basics
A quadratic function has the form f(x) = ax² + bx + c where a ≠ 0. Every quadratic function creates a U-shaped curve called a parabola when graphed. The standard form f(x) = a² + k tells you exactly where the parabola's lowest (or highest) point is.
The point (h, k) is called the vertex of the parabola. When a > 0, the parabola opens upward like a cup. When a < 0, it opens downward like an upside-down cup. Finding the vertex is crucial because it represents either the minimum or maximum value of the function.
To convert from general form to standard form, you need to "complete the square." This involves rearranging terms and adding/subtracting values to create a perfect square trinomial.
💡 Think of the standard form as giving you GPS coordinates for the vertex. The h tells you to go left/right, and the k tells you how high/low the vertex sits!
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
Graphing Quadratic Functions
When graphing a quadratic function, finding key points makes the process much easier. Start with the vertex - it's the turning point of your parabola. Then find the y-intercept by plugging in x = 0, which tells you where the parabola crosses the y-axis.
The x-intercepts can be found by setting f(x) = 0 and solving the equation. Not all quadratic functions have x-intercepts - it depends on whether the discriminant is positive, zero, or negative.
The domain of a quadratic function is always all real numbers (-∞, ∞), meaning you can input any value for x. The range depends on whether the parabola opens up or down. If it opens up, the range is .
🔍 Missing x-intercepts? Check the discriminant! If b² - 4ac < 0, your parabola never crosses the x-axis.
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
Maximum and Minimum Values
One of the most useful features of quadratic functions is their ability to model maximum or minimum values. The vertex (h, k) is where these extreme values occur. This is incredibly helpful for optimization problems!
If a > 0 (parabola opens upward), the function has a minimum value of k at x = h. This means the output value can never go below k. If a < 0 (parabola opens downward), the function has a maximum value of k at x = h, meaning the output can never exceed k.
For a quadratic function in standard form f(x) = a² + k, you can immediately identify whether it has a maximum or minimum and what that value is. This is why converting to standard form is so important in applications.
⭐ Remember: In any optimization problem involving a quadratic function, the vertex gives you the answer! It's either the maximum or minimum value you're looking for.
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
Finding Maximum and Minimum Values
When given a quadratic function in general form f(x) = ax² + bx + c, you can find the maximum or minimum without converting to standard form. The x-value where this occurs is always at x = -b/(2a).
To find the actual maximum or minimum value, simply evaluate the function at this x-value. If a > 0, you've found the minimum value. If a < 0, you've found the maximum value.
This shortcut is incredibly useful for test questions and real-world problems. Instead of going through the entire process of converting to standard form, you can quickly identify where the extreme value occurs and what that value is.
🚀 Quick tip: The formula x = -b/(2a) is a time-saver on tests! Memorize it to find the vertex x-coordinate without completing the square.
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
Application and Modeling
Quadratic functions appear everywhere in the real world! From the path of a thrown ball to profit models, these functions help us analyze situations where values increase and then decrease (or vice versa).
When working with application problems, identify the quantities being related and set up a quadratic function. Then find the maximum or minimum using the techniques we've learned. The vertex will often represent the optimal solution - like the maximum height of a projectile or the minimum cost of production.
For optimization problems, remember to check if any constraints exist. Sometimes the mathematical maximum or minimum might fall outside the practical range of values for the situation.
🌟 Real-life connection: Gas mileage often follows a quadratic pattern - too slow or too fast both waste fuel, while a medium speed maximizes efficiency!
Sign up to see the contentIt's free!
Access to all documents
Improve your grades
Join milions of students
Real-World Applications
Quadratic functions are perfect for modeling situations with a clear maximum or minimum. For example, the gas mileage problem shows how efficiency first increases with speed, reaches an optimal point, then decreases at higher speeds.
In the car example, the gas mileage function M(s) = -1/28s² + 3s - 31 models the relationship between speed (s) and miles per gallon (M). By finding the vertex, we can determine the optimal speed for maximum efficiency.
To solve such problems, identify the coefficient values (a, b, c) and use the formula x = -b/(2a) to find where the maximum or minimum occurs. Then substitute this value back into the original function to find the optimal result.
🚗 Next time you're driving, remember that your car's optimal fuel efficiency isn't at the lowest or highest speed, but somewhere in the middle - just like a quadratic function predicts!
We thought you’d never ask...
What is the Knowunity AI companion?
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
Where can I download the Knowunity app?
You can download the app in the Google Play Store and in the Apple App Store.
Is Knowunity really free of charge?
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
8
Smart Tools NEW
Transform this note into: ✓ 50+ Practice Questions ✓ Interactive Flashcards ✓ Full Practice Test ✓ Essay Outlines
Practice Test
Quiz
Flashcards
Essay
Similar Content
Absolute Value Inequalities
This is a very helpful document and is a very good review.
Algebra 2Solving Quadratics - Different Methods
Learn how to use the completing the square method, factoring, and using the quadratic formula to solve quadratic equations with step-by-step instructions.
Algebra 211th
Properties of Exponents and Radicals
Simple property rules for exponents and radicals. Algebra, Pre-calc, and Calculus.
Algebra 2College
Inequality
Learn how to do inequality
Algebra 21.7 Linear Inequalities in one Variable
inequalities in one variable, linear
Algebra 210th
Inverse Variation Notes
These are my notes about inverse variation in Algebra II. :-)
Algebra 2Most popular content: Standard Form of a Parabola
Most popular content in Algebra 1
Most popular content
Can't find what you're looking for? Explore other subjects.
Students love us — and so will you.
4.6/5
App Store
4.7/5
Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan S
iOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha Klich
Android user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
Anna
iOS user
I think it’s very much worth it and you’ll end up using it a lot once you get the hang of it and even after looking at others notes you can still ask your Artificial intelligence buddy the question and ask to simplify it if you still don’t get it!!! In the end I think it’s worth it 😊👍 ⚠️Also DID I MENTION ITS FREEE YOU DON’T HAVE TO PAY FOR ANYTHING AND STILL GET YOUR GRADES IN PERFECTLY❗️❗️⚠️
Thomas R
iOS user
Knowunity is the BEST app I’ve used in a minute. This is not an ai review or anything this is genuinely coming from a 7th grade student (I know 2011 im young) but dude this app is a 10/10 i have maintained a 3.8 gpa and have plenty of time for gaming. I love it and my mom is just happy I got good grades
Brad T
Android user
Not only did it help me find the answer but it also showed me alternative ways to solve it. I was horrible in math and science but now I have an a in both subjects. Thanks for the help🤍🤍
David K
iOS user
The app's just great! All I have to do is enter the topic in the search bar and I get the response real fast. I don't have to watch 10 YouTube videos to understand something, so I'm saving my time. Highly recommended!
Sudenaz Ocak
Android user
In school I was really bad at maths but thanks to the app, I am doing better now. I am so grateful that you made the app.
Greenlight Bonnie
Android user
I found this app a couple years ago and it has only gotten better since then. I really love it because it can help with written questions and photo questions. Also, it can find study guides that other people have made as well as flashcard sets and practice tests. The free version is also amazing for students who might not be able to afford it. Would 100% recommend
Aubrey
iOS user
Best app if you're in Highschool or Junior high. I have been using this app for 2 school years and it's the best, it's good if you don't have anyone to help you with school work.😋🩷🎀
Marco B
iOS user
THE QUIZES AND FLASHCARDS ARE SO USEFUL AND I LOVE Knowunity AI. IT ALSO IS LITREALLY LIKE CHATGPT BUT SMARTER!! HELPED ME WITH MY MASCARA PROBLEMS TOO!! AS WELL AS MY REAL SUBJECTS ! DUHHH 😍😁😲🤑💗✨🎀😮
Elisha
iOS user
This app is phenomenal down to the correct info and the various topics you can study! I greatly recommend it for people who struggle with procrastination and those who need homework help. It has been perfectly accurate for world 1 history as far as I’ve seen! Geometry too!
Paul T
iOS user