Tangent lines are special lines that touch a circle at...
Geometry736 views·Updated Aug 20, 2026·2 pagesIntroduction to Tangents - Geometry Unit 10 Lesson 1
Lauren@laurens.img
1
of 2
Tangent Lines and Circles
A tangent line touches a circle at exactly one point, called the point of tangency. The key property to remember is that a line is tangent to a circle if and only if it's perpendicular to the radius drawn to that point of tangency.
When determining if a line is tangent to a circle, we can use the Pythagorean theorem. If we have a right triangle formed by the radius, the distance from the center to the line, and the connecting segment, we can check if the equation works out. If a²+b²=c², then the line is tangent to the circle.
To find unknown values involving tangent lines, apply the Pythagorean theorem and solve for the unknown variable. For example, if you know two sides of the right triangle formed by the tangent and radius, you can find the third side.
Remember This! When a line is tangent to a circle, it forms a right angle (90°) with the radius at the point of tangency - this is the property that makes all tangent problems solvable!
2
of 2
More Tangent Properties
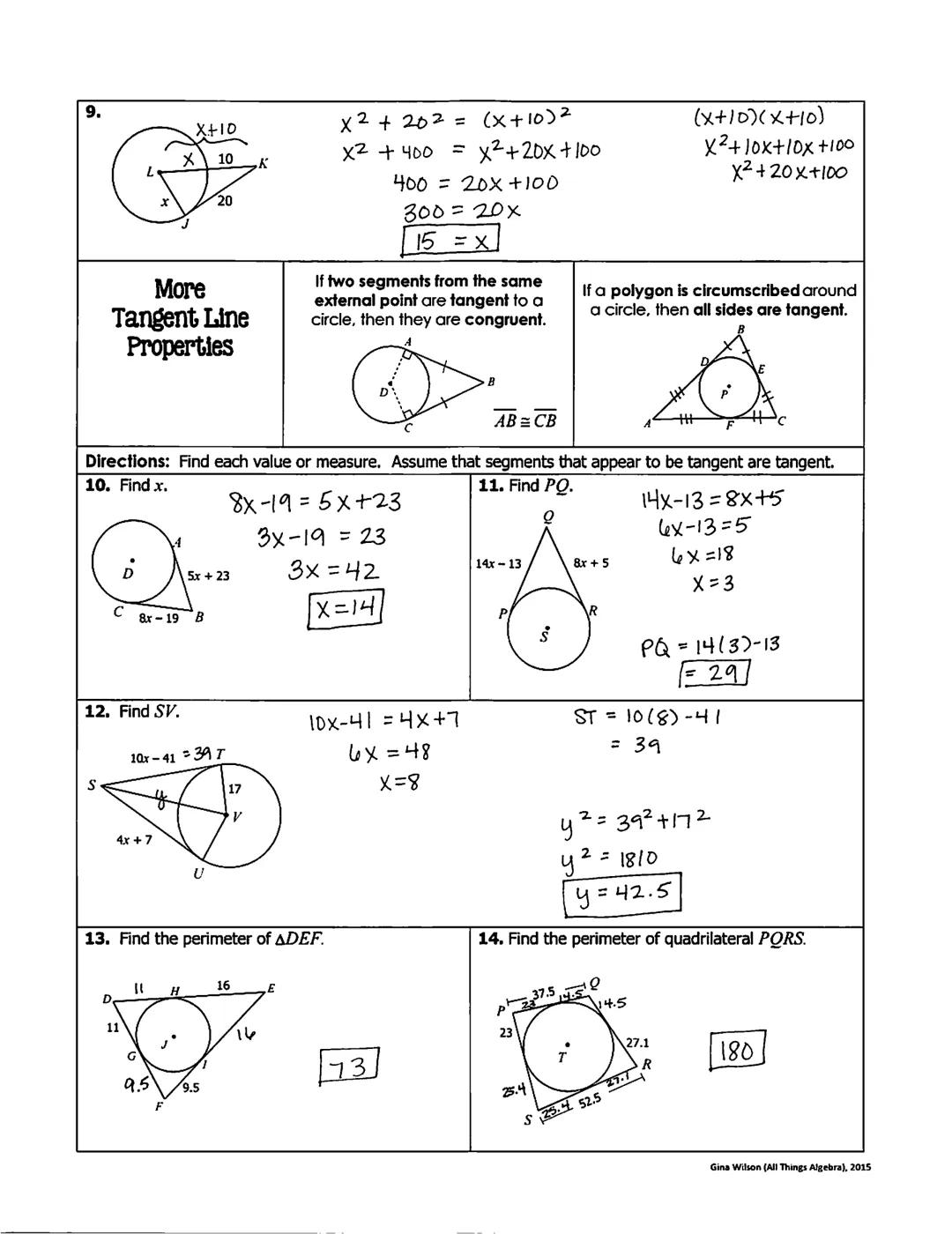
When two tangent segments extend from the same external point to a circle, they are congruent in length. This powerful property helps solve many geometry problems without needing to calculate every distance.
In a circumscribed polygon, all sides are tangent to the circle. This creates special relationships between the sides and the circle that can be used to find unknown measurements.
To solve tangent problems with variables, set up equations using the fact that tangent segments from the same point are equal in length. For example, if one tangent segment is and another is , you can set them equal and solve for x.
Pro Tip: When finding the perimeter of a polygon with sides tangent to a circle, remember that opposite tangent segments from the same point are equal - this can save you calculation steps!
We thought you’d never ask...
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
You can download the app in the Google Play Store and in the Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
Similar Content
Most popular content: Tangent
1Most popular content in Geometry
9GeometryGeometry Basics: Points, Lines, and Planes
Learn the fundamental concepts of geometry, including points, lines, and planes, and their properties and relationships.
9th3398
GeometryBasic Geometry Vocab
Just a couple of terms that are useful to know in Geometry
10th1500
GeometryParallel Lines cut by a Transveral
transversal, corresponding angles, alternate interior angles, alternate interior angles, alternate exterior angles, supplementary angles, vertical angles, consecutive interior angles/same side interior
10th811
GeometryIntroductory Geo Notes
Notes from first geometry class, meant for begginer students
8th611
GeometryUnit 10: Circles Homework 2: Central Angles & Arc Measures
Geometry Homework, 100%
10th1,9018
GeometryGeometry - Angles Notes
This tackles different angles in geometry and how to solve them.
7th27810
GeometryTrapezoids and lines
Trapezoid’s, isosceles trapezoid, mid segment of a trapezoid
862
GeometryGeometry Terms
Basic geometry terms and definitions
1547
GeometryGeometry Notes 9th Grade - Unit 1 A-1
Geometry Notes for Basic Geometry Vocabulary
9th720
Most popular content
9AlgebraFAR NOTES- CPM
Compiled by CPM
College2,11947
AP Physics 1Newton's Second Law of Motion
A detailed explanation of Concept of Newton's Second Law of Motion, Examples, Formulas, and Sample Problems with solution.
43614
AlgebraFAR NOTES-HERCULES
LAST MINUTE NOTES BY HERCULES CPA
College1,20218
AlgebraFAR NOTES - KUYA WOWOWIE
Far notes by Kuya Wowowie
College95118
EnglishIntroduction to linguistics
Introduction to linguistics exam revision notes. Structure of language, typologies of language, parts of speech, language families, Chomsky, Hockett, semantic triangle, Prague Linguistic Circle, writing systems, acquisition and learning
1,28253
AlgebraRFBT NOTES- HERCULES
LAST MINUTE NOTES BY HERCULES CPA
College92216
Fun StuffDMV Practice Test 1
First set of Questions from DMV Handbook
1,385131
AlgebraAFAR NOTES- CPM
Compiled by CPM
College1,31817
PhysicsTranslational Motion and Rotational Motion
Applications of Translational and Rotational Motion
11th1811
Students love us — and so will you.
4.6/5App Store
4.7/5Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan SiOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha KlichAndroid user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
AnnaiOS user
Geometry736 views·Updated Aug 20, 2026·2 pagesIntroduction to Tangents - Geometry Unit 10 Lesson 1
Lauren@laurens.img
Tangent lines are special lines that touch a circle at exactly one point. Understanding how tangents work and applying their properties helps solve various geometry problems. Let's explore how to identify tangent lines and use their properties in different situations.
1
of 2
Sign up to see the content. It's free!
- Access to all documents
- Improve your grades
- Join milions of students
Tangent Lines and Circles
A tangent line touches a circle at exactly one point, called the point of tangency. The key property to remember is that a line is tangent to a circle if and only if it's perpendicular to the radius drawn to that point of tangency.
When determining if a line is tangent to a circle, we can use the Pythagorean theorem. If we have a right triangle formed by the radius, the distance from the center to the line, and the connecting segment, we can check if the equation works out. If a²+b²=c², then the line is tangent to the circle.
To find unknown values involving tangent lines, apply the Pythagorean theorem and solve for the unknown variable. For example, if you know two sides of the right triangle formed by the tangent and radius, you can find the third side.
Remember This! When a line is tangent to a circle, it forms a right angle (90°) with the radius at the point of tangency - this is the property that makes all tangent problems solvable!
2
of 2Sign up to see the content. It's free!
- Access to all documents
- Improve your grades
- Join milions of students
More Tangent Properties
When two tangent segments extend from the same external point to a circle, they are congruent in length. This powerful property helps solve many geometry problems without needing to calculate every distance.
In a circumscribed polygon, all sides are tangent to the circle. This creates special relationships between the sides and the circle that can be used to find unknown measurements.
To solve tangent problems with variables, set up equations using the fact that tangent segments from the same point are equal in length. For example, if one tangent segment is and another is , you can set them equal and solve for x.
Pro Tip: When finding the perimeter of a polygon with sides tangent to a circle, remember that opposite tangent segments from the same point are equal - this can save you calculation steps!
We thought you’d never ask...
Our AI companion is specifically built for the needs of students. Based on the millions of content pieces we have on the platform we can provide truly meaningful and relevant answers to students. But its not only about answers, the companion is even more about guiding students through their daily learning challenges, with personalised study plans, quizzes or content pieces in the chat and 100% personalisation based on the students skills and developments.
You can download the app in the Google Play Store and in the Apple App Store.
That's right! Enjoy free access to study content, connect with fellow students, and get instant help – all at your fingertips.
Similar Content
Most popular content: Tangent
1Most popular content in Geometry
9GeometryGeometry Basics: Points, Lines, and Planes
Learn the fundamental concepts of geometry, including points, lines, and planes, and their properties and relationships.
9th3398
GeometryBasic Geometry Vocab
Just a couple of terms that are useful to know in Geometry
10th1500
GeometryParallel Lines cut by a Transveral
transversal, corresponding angles, alternate interior angles, alternate interior angles, alternate exterior angles, supplementary angles, vertical angles, consecutive interior angles/same side interior
10th811
GeometryIntroductory Geo Notes
Notes from first geometry class, meant for begginer students
8th611
GeometryUnit 10: Circles Homework 2: Central Angles & Arc Measures
Geometry Homework, 100%
10th1,9018
GeometryGeometry - Angles Notes
This tackles different angles in geometry and how to solve them.
7th27810
GeometryTrapezoids and lines
Trapezoid’s, isosceles trapezoid, mid segment of a trapezoid
862
GeometryGeometry Terms
Basic geometry terms and definitions
1547
GeometryGeometry Notes 9th Grade - Unit 1 A-1
Geometry Notes for Basic Geometry Vocabulary
9th720
Most popular content
9AlgebraFAR NOTES- CPM
Compiled by CPM
College2,11947
AP Physics 1Newton's Second Law of Motion
A detailed explanation of Concept of Newton's Second Law of Motion, Examples, Formulas, and Sample Problems with solution.
43614
AlgebraFAR NOTES-HERCULES
LAST MINUTE NOTES BY HERCULES CPA
College1,20218
AlgebraFAR NOTES - KUYA WOWOWIE
Far notes by Kuya Wowowie
College95118
EnglishIntroduction to linguistics
Introduction to linguistics exam revision notes. Structure of language, typologies of language, parts of speech, language families, Chomsky, Hockett, semantic triangle, Prague Linguistic Circle, writing systems, acquisition and learning
1,28253
AlgebraRFBT NOTES- HERCULES
LAST MINUTE NOTES BY HERCULES CPA
College92216
Fun StuffDMV Practice Test 1
First set of Questions from DMV Handbook
1,385131
AlgebraAFAR NOTES- CPM
Compiled by CPM
College1,31817
PhysicsTranslational Motion and Rotational Motion
Applications of Translational and Rotational Motion
11th1811
Students love us — and so will you.
4.6/5App Store
4.7/5Google Play
The app is very easy to use and well designed. I have found everything I was looking for so far and have been able to learn a lot from the presentations! I will definitely use the app for a class assignment! And of course it also helps a lot as an inspiration.
Stefan SiOS user
This app is really great. There are so many study notes and help [...]. My problem subject is French, for example, and the app has so many options for help. Thanks to this app, I have improved my French. I would recommend it to anyone.
Samantha KlichAndroid user
Wow, I am really amazed. I just tried the app because I've seen it advertised many times and was absolutely stunned. This app is THE HELP you want for school and above all, it offers so many things, such as workouts and fact sheets, which have been VERY helpful to me personally.
AnnaiOS user